Diese Seite befindet sich im Aufbau

MATH+ projects

• Uncertainty Quantification and Design of Experiments for Data-Driven Control
• Machine Learning Enhanced Filtering Methods for Inverse Problems
• Wasserstein Gradient Flows for Generalised Transport in Bayesian Inversion

Uncertainty quantification for PDEs using quasi-Monte Carlo methods

Modern quasi-Monte Carlo (QMC) methods are based on tailoring specially designed cubature rules for high-dimensional integration problems. By leveraging the smoothness and anisotropy of an integrand, it is possible to achieve faster-than-Monte Carlo convergence rates. QMC methods have become a popular tool for solving partial differential equations (PDEs) involving random coefficients, a central topic within the field of uncertainty quantification.

Problems in uncertainty quantification can be roughly divided into two categories. Forward uncertainty quantification is the study of how uncertainties in mathematical or computational models and their inputs affect the system response. Conversely, inverse uncertainty quantification is concerned with the inverse problem of estimating the system inputs based on observations of the response of the system. In both cases, state-of-the-art cubature rules are essential to make the quantification of uncertainty tractable in practice.

Click the image to play the animation

Publications

Peer-reviewed papers

• I. H. Sloan and V. Kaarnioja. Doubling the rate – improved error bounds for orthogonal projection with application to interpolation. Accepted for publication in BIT Numer. Math. Preprint: arXiv:2308.06052 [math.NA]
• V. Kaarnioja and A. Rupp. Quasi-Monte Carlo and discontinuous Galerkin. Electron. Trans. Numer. Anal. 60:589–617, 2024. https://doi.org/10.1553/etna_vol60s589
• V. Kaarnioja, F. Y. Kuo, and I. H. Sloan. Lattice-based kernel approximation and serendipitous weights for parametric PDEs in very high dimensions. In: Monte Carlo and Quasi-Monte Carlo Methods 2022, A. Hinrichs, P. Kritzer, F. Pillichshammer (eds.), Springer Verlag, pp. 81–103, 2024. https://doi.org/10.1007/978-3-031-59762-6_4
• P. A. Guth and V. Kaarnioja. Application of dimension truncation error analysis to high-dimensional function approximation in uncertainty quantification. In: Monte Carlo and Quasi-Monte Carlo Methods 2022, A. Hinrichs, P. Kritzer, F. Pillichshammer (eds.), Springer Verlag, pp. 297–312, 2024. https://doi.org/10.1007/978-3-031-59762-6_14
• P. A. Guth and V. Kaarnioja. Generalized dimension truncation error analysis for high-dimensional numerical integration: lognormal setting and beyond. SIAM J. Numer. Anal. 62(2): 872–892, 2024. https://doi.org/10.1137/23M1593188
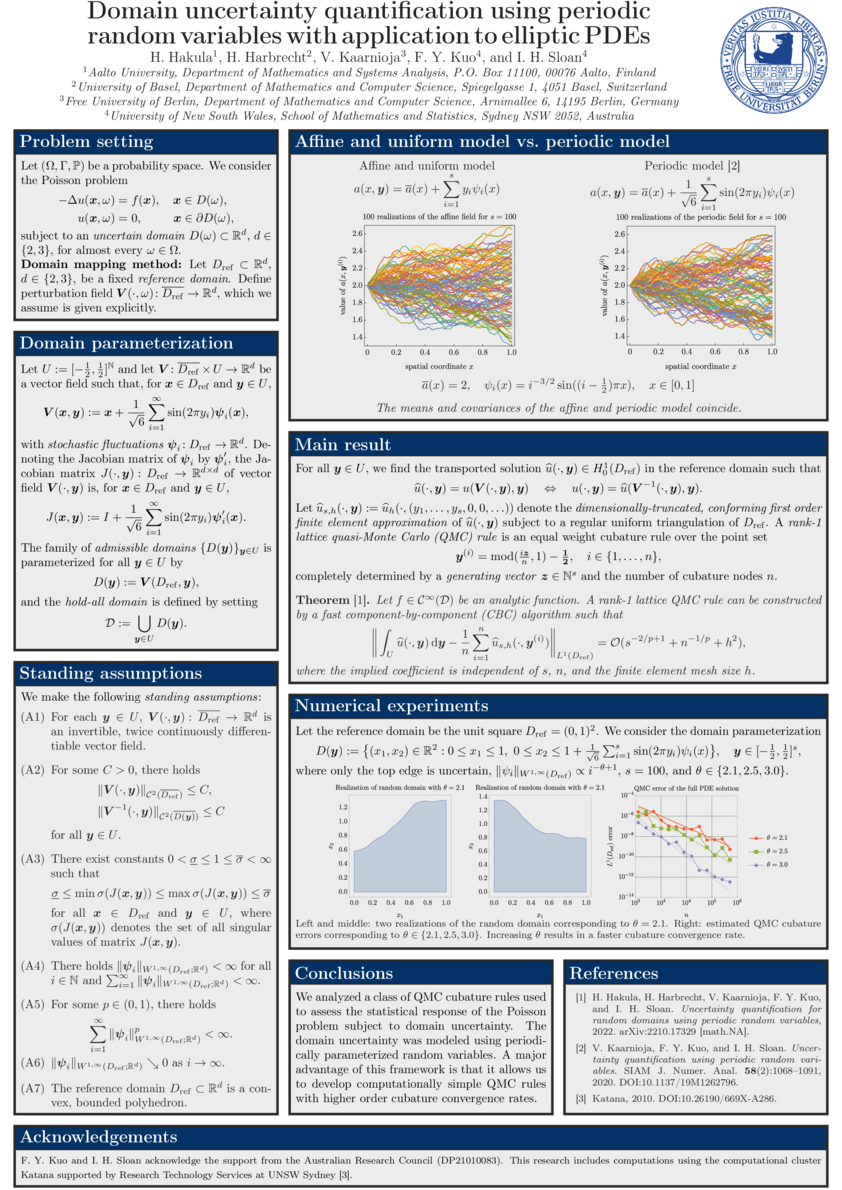
• H. Hakula, H. Harbrecht, V. Kaarnioja, F. Y. Kuo, and I. H. Sloan. Uncertainty quantification for random domains using periodic random variables. Numer. Math. 156:273–317, 2024. https://doi.org/10.1007/s00211-023-01392-6

Submitted manuscripts

• L. Bazahica, V. Kaarnioja, and L. Roininen. Uncertainty quantification for electrical impedance tomography using quasi-Monte Carlo methods. Preprint 2024. arXiv:2411.11538 [math.NA]
• P. A. Guth and V. Kaarnioja. Quasi-Monte Carlo for partial differential equations with generalized Gaussian input uncertainty. Preprint 2024. arXiv:2411.03793 [math.NA]

Miscellaneous

• H. Hakula, H. Harbrecht, V. Kaarnioja, F. Y. Kuo, and I. H. Sloan. Domain uncertainty quantification using periodic random variables with application to elliptic PDEs. Poster presented at Bayes Comp 2023, Levi, Finland, March 15, 2023.

Click to enlarge the image

Optimal control and optimal design problems governed by PDEs with uncertain coefficients

In PDE-constrained optimal control problems, the target function is the solution of a PDE, steered by a control function. However, if the material properties of a mathematical model are poorly known or even completely unknown, it may be necessary to model these uncertainties using random fields.

To account for the presence of uncertainty in optimal control problems, one may compose the objective with a risk measure. Risk measures such as the expected value or the entropic risk measure involve high-dimensional integrals over the stochastic variables. This leads to challenging high-dimensional integration problems, which may be tackled using, e.g., QMC methods.

Meanwhile, optimal experimental design involves designing a measurement configuration (for example, finding the optimal placement of sensors to collect observational data) to maximize the information gained from an experiment. The Bayesian approach to optimal design can be used to maximize the information gained from the data while minimizing resources and costs. This approach leads to challenging high-dimensional integration problems that can be efficiently approximated using QMC or other higher-order cubature methods.

Click the image to play the animation

Publications

Peer-reviewed papers

• P. A. Guth, V. Kaarnioja, F. Y. Kuo, C. Schillings, and I. H. Sloan. Parabolic PDE-constrained optimal control under uncertainty with entropic risk measure using quasi-Monte Carlo integration. Numer. Math. 156:565–608, 2024. https://doi.org/10.1007/s00211-024-01397-9

Submitted manuscripts

• V. Kaarnioja and C. Schillings. Quasi-Monte Carlo for Bayesian design of experiment problems governed by parametric PDEs. Preprint 2024. arXiv:2405.03529 [math.NA]

Miscellaneous

• P. A. Guth, V. Kaarnioja, F. Y. Kuo, C. Schillings, and I. H. Sloan. Quasi-Monte Carlo methods for optimal control problems subject to parabolic PDE constraints under uncertainty. Poster presented at Symposium on Inverse Problems: From experimental data to models and back, University of Potsdam, September 19, 2022.

Click to enlarge the image